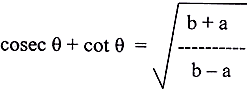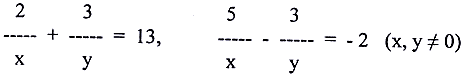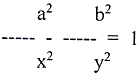Section – C
13. On dividing x2 – x3 – 3x2 + 3x + 2 by a polynomial g(x), the quotient and remainder were x2 – x – 2 and 2x respectively. Find g(x).
14. In Δ ABC, if EF || AB and ar (Δ CEF) = ar (EFBA), then find ration of CA and EA.
15. If b cos θ = a, then prove that
16. If (2,5), (3, 4) and (x, y) are collinear, show that x + y = 7.
17. If α and ß are zeroes of a quadratic polynomial 4x2 + 4x + 1, then form a quadratic polynomial whose zeroes are 2α and 2ß.
18. The sum of 7th and 3rd terms of an A.P is 6 and their product is 8. Find the sum of first 20 terms of the A.P.
19. Check whether the question 5x2 + 6x – 2 = 0 has real roots and if it has, find them by the method of completing the square.
20. Three takers contain 187 l, and 275 l of petrol respectively. Using Euclid’s division algorithm find the capacity of the largest container that can measure the petrol of the three containers exact number of times.
21. Solve the following pair of liner equations for x and y.
22. If x = a sin θ and y = b tan θ, then show that
Section – D
23. As observed from the top of a 100 m high light house from the sea level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships. (Use √3 = 1.732).
24. If in a triangle, the square of one side is equal to the sum of the squares of the remaining two sides, prove that the angle opposite to the first side is a right angle.
25. Find all zeroes of the polynomial (2x4 – 9x3 + 5x2 + 3x -1) if two of its zeroes are (2 + √3) and (2 – √3).
26. Draw the graphs of the equations: 4x – 3y – 6 = 0 and x + 3y – 9 = 0. Also determine the vertices of the triangle formed by the lines and the y axis.
27. A motorboat whose speed is 18 km/hr in still water takes 1 hr more to go 24 km upstream than to return downstream to the spot. Find the speed of the stream.
28. Prove that the points (0, 0), (5, 5) and (- 5, 5) are the vertices of an isosceles triangle. Find the length of the hypotenuse and also find its area.
29. Divide 56 in four parts in A.P such that the ratio of the product of the extremes to the product of means is 5 : 6.
30. Prove that (sin θ + cos θ + 1). (sin θ – 1 + cos θ). sec θ. cosec θ = 2.
 Class Notes NCERT Solutions for CBSE Students
Class Notes NCERT Solutions for CBSE Students