10th Class CBSE Mathematics 2018-19
M.M.: 80
Class: 10th
Subject: Mathematics
Date: 07/03/2019
General Instructions:
- All questions are compulsory.
- This question paper consists of 30 questions divided into four sections – A, B, C and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each.
- There is no overall choice. However, an internal choice has been provided in two questions of 1 marks two questions of 2 marks, four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternative in all such questions.
- Use of calculator is not permitted.
Section A
Question numbers 1 to 6 carry 1 mark each.
Question: 1. Two positive integers a and b can be written as a = x²y² and b = xy³. x, y are prime numbers. Find LCM (a, b).
Question: 2. How many two digits numbers are divisible by 3?
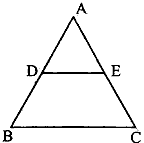
Question: 3. In fig. 1, DE||BC, AD = 1 cm and BD = 2 cm. What is the ratio of the ar (Δ ABC) to the ar (Δ ADE)?
Question: 4. Find the coordinates of a point A, where AB is diameter of a circle whose center is (2, -3) and B is the point (1, 4).
Question: 5. For what values of k, the roots of the equation x² + 4x + k = 0 are real?
Or
Find the value of k for which the roots of the equation 3x² – 10x + k = 0 are reciprocal of each other.
Question: 6. Find A if tan 2A = cot (A – 24°)
Or
Find the value of (sin² 33° + sin² 57°)
Section B
Question numbers 7 to 12 carry 2 marks each.
Question: 7. Find, how many two digit natural numbers are divisible by 7.
Or
If the sum of first n terms of an AP is n², then find its 10th terms.
Question: 8. A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game.
Question: 9. Find the ratio in which the segment joining the points (1, -3) and (4, 5) is divided by x-axis? Also find the coordinates of this point on x-axis?
Question: 10. A die is thrown once. Find the probability of getting a number which (i) is a prime number (ii) lies between 2 and 6.
Question: 11. Find c if the system of equations cx + 3y + (3 – c) = 0; 12x + cy – c = 0 has infinitely many solutions?
Question: 12. Find the HCF of 1260 and 7344 using Euclid’s algorithm.
Or
Show that every positive odd integer is of the form (4q + 1) or (4q + 3), where q is some integer.
Section C
Question number 13 to 22 carry 3 marks each.
Question: 13. Find all zeros of the polynomial 13. 3x³ + 10x² – 9x – 4 if one its zero is 1.
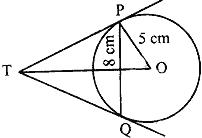
Question: 14. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at p and Q intersect at a point T (see Fig. 2). Find the length TP.
Question: 15. Prove that 2+√3/5 is an irrational number, given that √3 is an irrational number.
Question: 16. Prove that (sin θ + cosec θ)² + (cos θ + sec θ)² = 7 + tan² θ + cot² θ.
Or
Prove that (1 + cot A – cosec A) (1 + tan A + sec A) = 2
Question: 17. A father’s age is three times the sum of the ages of his two children. After 5 years his age will be two times the sum of their ages. Find the present age of the father.
Or
A fraction becomes 1/3 when 2 is subtracted from the numerator and it becomes 1/2 when 1 is subtracted from the denominator. Find the fraction.
Question: 18. Find the point on y-axis which is equidistant from the points (5, – 2) and (-3. 2).
Or
The line segment joining the points A(2, 1) and B(5, -8) trisected at the points P and Q such that Pis nearer to A. If P also lies on the line given by 2x – y + k = 0, find the value of k.
Question: 19. Find the made of the following frequency distribution.

Question: 20. Water in a canal, 6 m wide and 1.5 m deep, is flowing with speed of 10 km/hour. How much area will it irrigate in 30 minutes; If 8 cm standing water is needed?
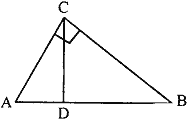
Question: 21. In fig. 3, ∠ ACB = 90° and CD⊥ AB, prove that CD² = BD × AD.
Or
If P and Q are the points on side CA and CB respectively of Δ ABCD, right angled at C. Prove that (AQ² + BP²) = (AB² + PQ²)
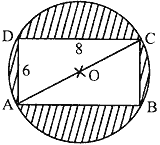
Question: 22. Find the area of the shaded region in Fig. 4, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of circle. (Take π = 3.14)
Question: 23.
Question: 24. Prove that the ration of the two similar triangle is equal to the square of the ratio of their corresponding sides.
Question: 25. The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to a ‘less than type’ cumulative frequency distribution and draw its ogive.
Or
The table shows the daily expenditure on food of 25 households in a locality. Find the mean daily expenditure on food.

 Class Notes NCERT Solutions for CBSE Students
Class Notes NCERT Solutions for CBSE Students





