10th Mathematics Periodic Test III (2018-19)
Time: 3 hours
M.M: 80
Subject Code: 041
Class: X
Subject: Mathematics
Date: 21.01.2019
General Instructions:
- All questions are compulsory.
- The question paper consist of 30 questions divided into four section A, B, C, and D. Section A comprise of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of of 3 marks each and Section D comprises of 8 questions of 4 marks each.
- Use of calculator is not permitted.
Section A
Question: 1. The nth term an AP is 7 – 4n. Find its common difference.
Question: 2. What is the HCF of smallest prime number and the smallest composite number?
Question: 3. Find the distance of the point (-8, 6) from the origin.
Question: 4. Write the polynomial whose zeroes are 2 +√3 and 2 – √3.
OR
If (x + a) is a factor of 2x2 + 2ax + 5x + 10 = 0, then find the value of a.
Question: 5. Find the value of cos267° – sin223°.
OR
If tanθ = cot (30° + θ), find the value of θ.
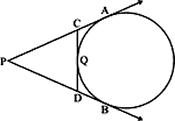
Question: 6. In the given figure, PA and PB are tangents to the circle. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2cm, what is the length of PC?
Section B
Question: 7. A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. Find the probability of getting:
(a) A white ball or green ball (b) Neither a green ball nor a red ball.
Question: 8. Determine the value of m and n, so that the following system of linear equations has infinite number of solutions:
(2m – 1)x + 3y – 5 = 0
3x + (n – 1)y – 2 = 0
Question: 9. Show that the square of any positive integer is of the form 3m or 3m + 1 for some integer m.
OR
Prove that 8+9√7 is an irrational number, given that √7 is irrational.
Question: 10. If the distances of P(x,y) from the points A(3,6) and B(-3,4) are equal, prove that 3x + y = 5.
Question: 11. A game consists of tossing a one-rupee coin three times and nothing its outcome each time. Find the probability of getting
(a) atleast two tails (b) three heads
Question: 12. How many terms of the AP 18, 16, 14…. should be taken so that their sum is zero?
OR
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Section C
Question: 13. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Question:14. If 4tanθ = 3, evaluate 4sinθ – cosθ + 1/4sinθ + cosθ – 1
OR
If tan(A+B) = √3 and tan(A-B) – 1/√3, find A and B.
Question: 15. Size of agriculture holding in a survey of 200 families is given in the following table:

Computer the mode size of holding.
 Class Notes NCERT Solutions for CBSE Students
Class Notes NCERT Solutions for CBSE Students